No more vendor spreadsheets with transcribed dimensions and inconsistent computations.

Vendors provide measurement data, AND THAT'S IT. Statistical computations on the measurement data, and generation of reports and graphs, are all done by balloonDigest. You get the same reliable state of the art analysis, done the same way and in the same format every single time.

• Load a 2D drawing which has balloon meta data. Use balloonDigest to rapidly find balloons.
• Load vendor data and watch balloonDigest bring your 2D drawing to life, coloring FAI and SPC balloons according to the performance of the data. Each balloon becomes a clickable button which shows the data in detail.

This magic is accomplished by an initial meta data saving step that only needs to be done once. Meta data is entered for each balloon, and saved to the drawing. For detail on this and additional aspects of the workflow, please visit our operational details page.

Balloons are colored based on statistics of the associated data.

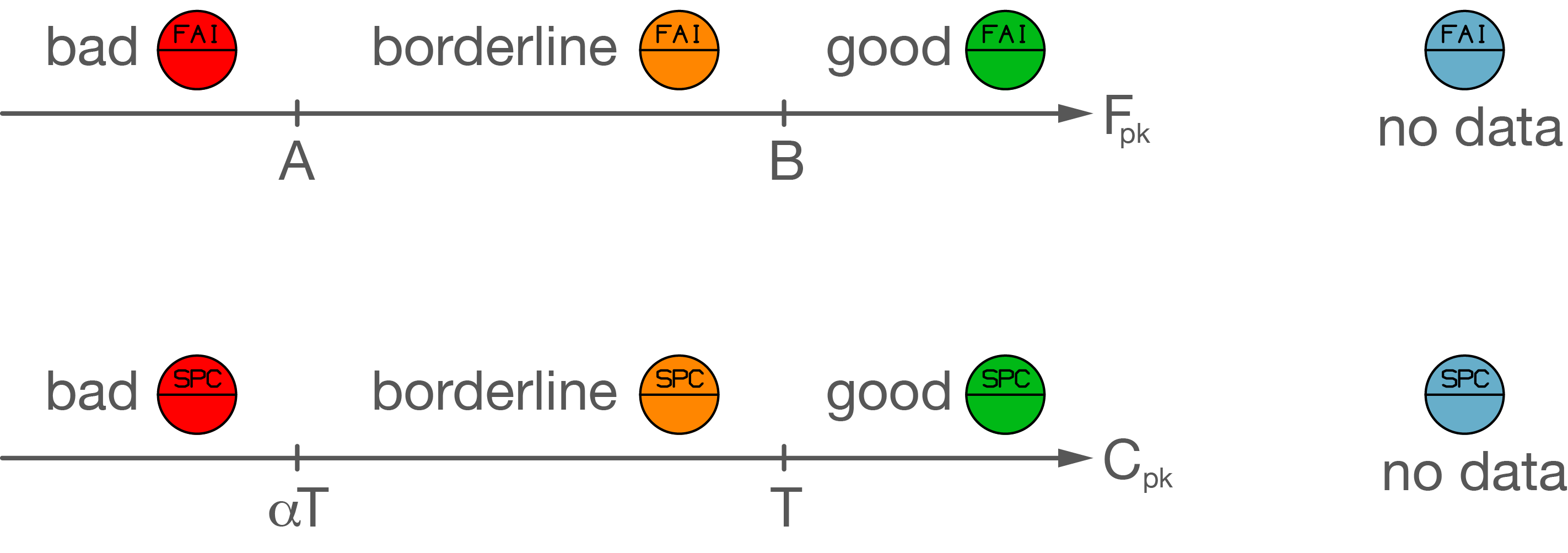
where T is the per-balloon $C_{pk}$ target.

A =

B =

$\alpha$ =

For FAI data on a bilateral spec, we introduce $$F_{pk}=\min\left\{\frac{a-LSL}{USL-LSL},\frac{USL-b}{USL-LSL}\right\},$$ where $a$ and $b$ are the minimum and maxium data values, and where $LSL$ and $USL$ are the lower and upper spec limits on the dimension. The higher the value of $F_{pk}$ the better, with a best possible value of 0.5. Here are some examples:

For FAI data on a unilateral spec, we introduce $$F_{pk}=\frac{USL-b}{2\cdot USL},$$ where $b$ is the maxium data value, and where $USL$ is the upper spec limit on the dimension. As with the bilateral case, the higher the value of $F_{pk}$ the better, with a best possible value of 0.5. Here are some examples:

For SPC data on a bilateral spec, we use $$C_{pk}=\min\left\{\frac{\mu-LSL}{3\sigma},\frac{USL-\mu}{3\sigma}\right\},$$ where $\mu$ and $\sigma$ are the mean and standard deviation of the data, and where $LSL$ and $USL$ are the lower and upper spec limits on the dimension. As with $F_{pk}$, higher values of $C_{pk}$ are better. Here are some examples:

For SPC data on a unilateral spec, we use $$C_{pk}=\frac{USL-\mu}{3\sigma},$$ where $\mu$ and $\sigma$ are the mean and standard deviation of the data, and where $USL$ is the upper spec limit on the dimension. As with the bilateral case, higher values of $C_{pk}$ are better. Here are some examples:

A bilateral dimension is one that makes physical sense for values greater and less than the nominal (ideal) target value.

A unilateral dimension is one that doesn't make physical sense for values either greater than or less than the nominal value. For instance, concentraction can never be more than 100%, and flatness can never be less than 0. Unilateral dimensions on mechanical parts seem to consist exclusively of values that are ideally zero, but that stray positive because of imperfections, (e.g., flatness, perpendicularity, cylindricity, profile tolerance, etc).

Most bilateral values arise from of a sequence of independant random processes, and as a result are normally distributed. Unilateral values aren't so simple. Consider throwing darts at a target, and keeping track of the distance the darts are from the target center. Suppose that for any set of axes you may establish on the 2D target surface, the x coordinates of the dart locations are normally distributed. Then, the squares of the distances of the dart locations to the target center will have a Chi-squared distribution with 2 degrees of freedom. In the case of an N dimensional target, the Chi-squared distribution will have N degrees of freedom. Unilateral dimensions on mechanical parts correspond to an N dimensional target, where N varies depending on the details of the processes used to create the part.

FAI and SPC data enters balloonDigest by way of a single .csv file. The format requirements are simple- essentially the file needs to look like the sample below. An example of a properly formatted vendor data .csv file can be downloaded here.

Part Number	200-12345-000
Part Name	exceptional part
Vendor	some vendor
Date	YYYY.MM.DD
Part Info	xyz
Balloon Type	Balloon ID	Location #
FAI	23	1	3.145	3.235	3.055
FAI	23	2	3.211	3.212	3.324
FAI	23	3	3.532	3.132	3.344
SPC	12	1	33.245	33.032	33.179	33.865	33.976	...	33.054
SPC	16	1	23.876	24.032	24.179	23.980	23.982	...	24.021
FAI	4	1	7.988	7.796	7.832

All of the balloon digest processing occurs on the client side (i.e., your computer). No PDF or vendor data is sent to any server.

Please send any questions and comments about balloonDigest to balloondigest@gmail.com